Equilíbrio de um corpo extenso

Momento escalar de uma força 

Como vimos no tópico anterior, existe a possibilidade de rotação em um corpo extenso. Para que a força cause uma rotação do corpo extenso, deve ocorrer uma grandeza física denominada momento escalar. 


Vejamos um corpo extenso que é capaz de girar em torno do ponto O, tendo assim uma força F, que é aplicada no corpo. 


Vejamos a ilustração: 

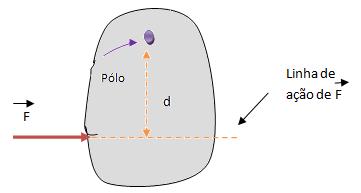
Com base na figura acima, podemos perceber que há uma distância d, que representa a distância que vai do ponto O até a linha de ação de F, que é denominada braço de força, enquanto o ponto O é denominado pólo. 


Através de uma equação podemos definir a relação entre o momento escalar (M) da força e o pólo O. 


Vejamos a equação: 





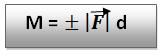
Com relação ao sinal do momento escalar, devemos saber que ele irá depender do sentido em que a rotação está, ou seja, irá depender do sentido em que a força tender a girar o corpo.


Binário 
O binário é considerado um sistema composto por duas forças, com a mesma direção e a mesma intensidade, porém com sentidos opostos, contendo também uma linha de ação não- coincidente.
 
Vejamos:



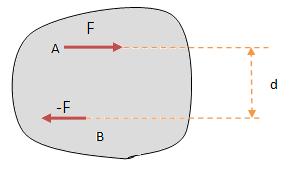
Como podemos perceber no binário acima, há uma distância entre as forças, essa distância é denominada braço binário. 


A força de um binário é considerada nula, pois o corpo não tem a tendência de acelerar quando está em movimento de translação. 


Já se pensarmos no momento escalar de um binário, devemos saber que sua intensidade com relação a todos os pólos será dada através de: |F| d. 
Quanto à ação do binário, é importante sabermos que ele se limita a causar um movimento de rotação acelerado no corpo extenso. 


Condições de equilíbrio 


Existem duas condições para que um corpo extenso esteja em equilíbrio. Sendo elas: 


Todas resultantes das forças externas do corpo serão nulas. 


Quando falamos das somas forças, externas que agem sobre o corpo, devemos saber que elas são todas nulas com reação aos pólos. 
Agora se tratando do equilíbrio, vejamos: 


Quando falamos da condição 1, estamos nos referindo a um equilíbrio translatório, já quando falamos da condição 2, estamos nos referindo a um equilíbrio rotatório. 


Com isso podemos ver que a condição 2 não irá existir em um ponto material, pois não há chances de ocorrer o movimento de rotação.